Steven J. Barnett

Last week I worked on an implementation of the GJK and EPA agorithms using purely mathematical volumes. Each shape is defined only by a find_furthest (or get_support) function, which returns its extent in a direction.

While this is a nice and useful way to define geometry for those particular interference algorithms, it would be really nice to be able to actually see the geometry for debugging. To do this, a mesh approximation must be generated using only a find_furthest function.

My idea is to use an algorithm similar to an icosphere generator. Here’s an outline of the modified algorithm:

1. Start with an icosahedron and push each vertex to the extents of the object.
2. For each triangle, if it has an area larger than some minimum, subdivide it into four triangles.
3. For each pair of vertexes which are closer than some maximum, combine them into one.
4. Repeat steps 2 & 3 until step 2 produces no triangles.

The only subtlety is in step 2, where I subdivide based on the “normalized” vertexes of the shape (which are just the vertexes of triangles on a unit icosphere).

The idea is to quickly generate a mesh which fills in high-detail areas with more polygons and leaves planar areas simple. It should result in a mesh with higher poly count in areas of higher detail.

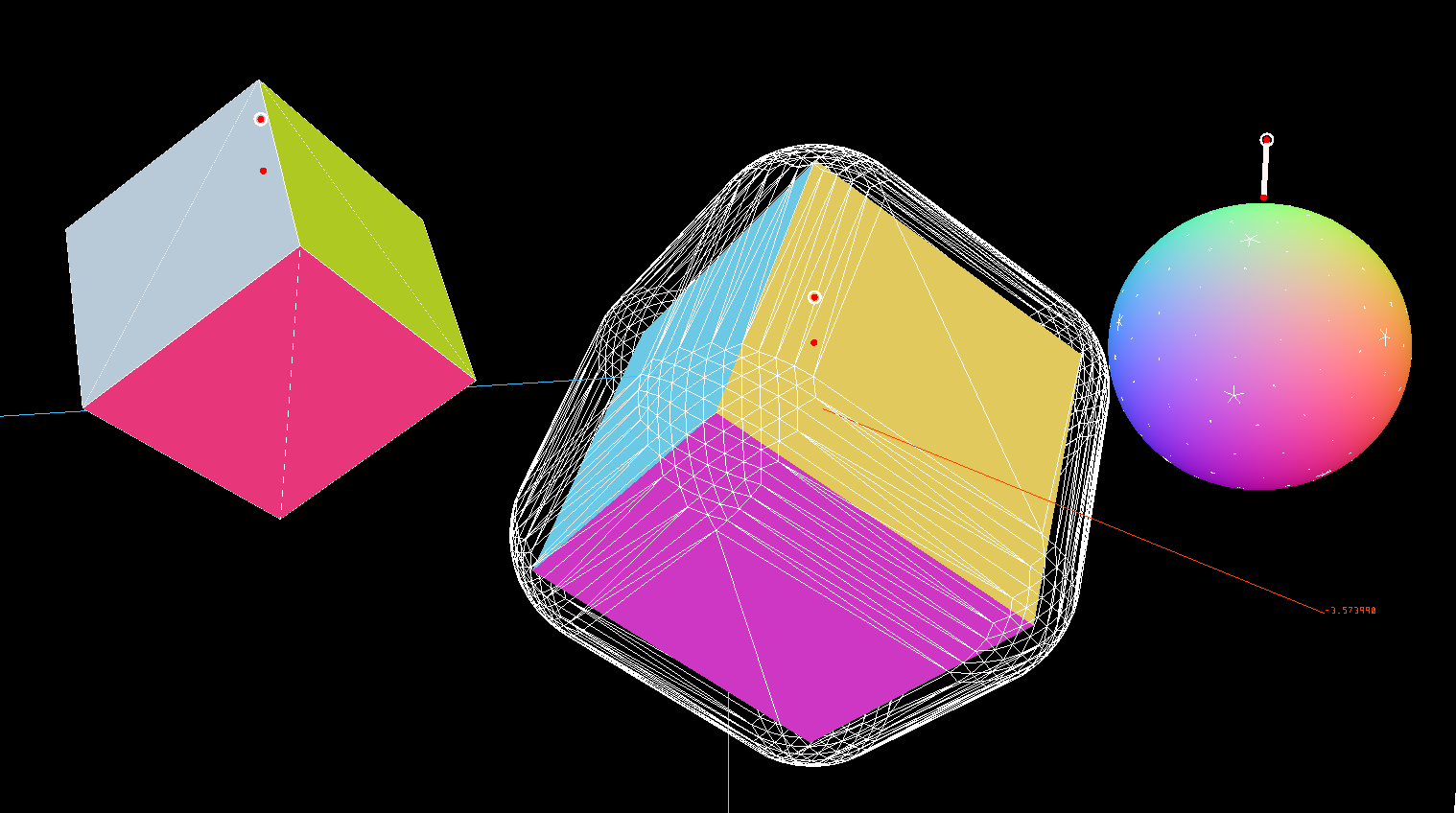
In this shot, three different geometries were meshed using this method - they are drawn using white wireframes. A cube, a sphere, and a sphere-swept cube (which is just the Minkowski sum of the two). The wireframe for the plain old sphere is mostly masked by its non-debug mesh in this picture :P

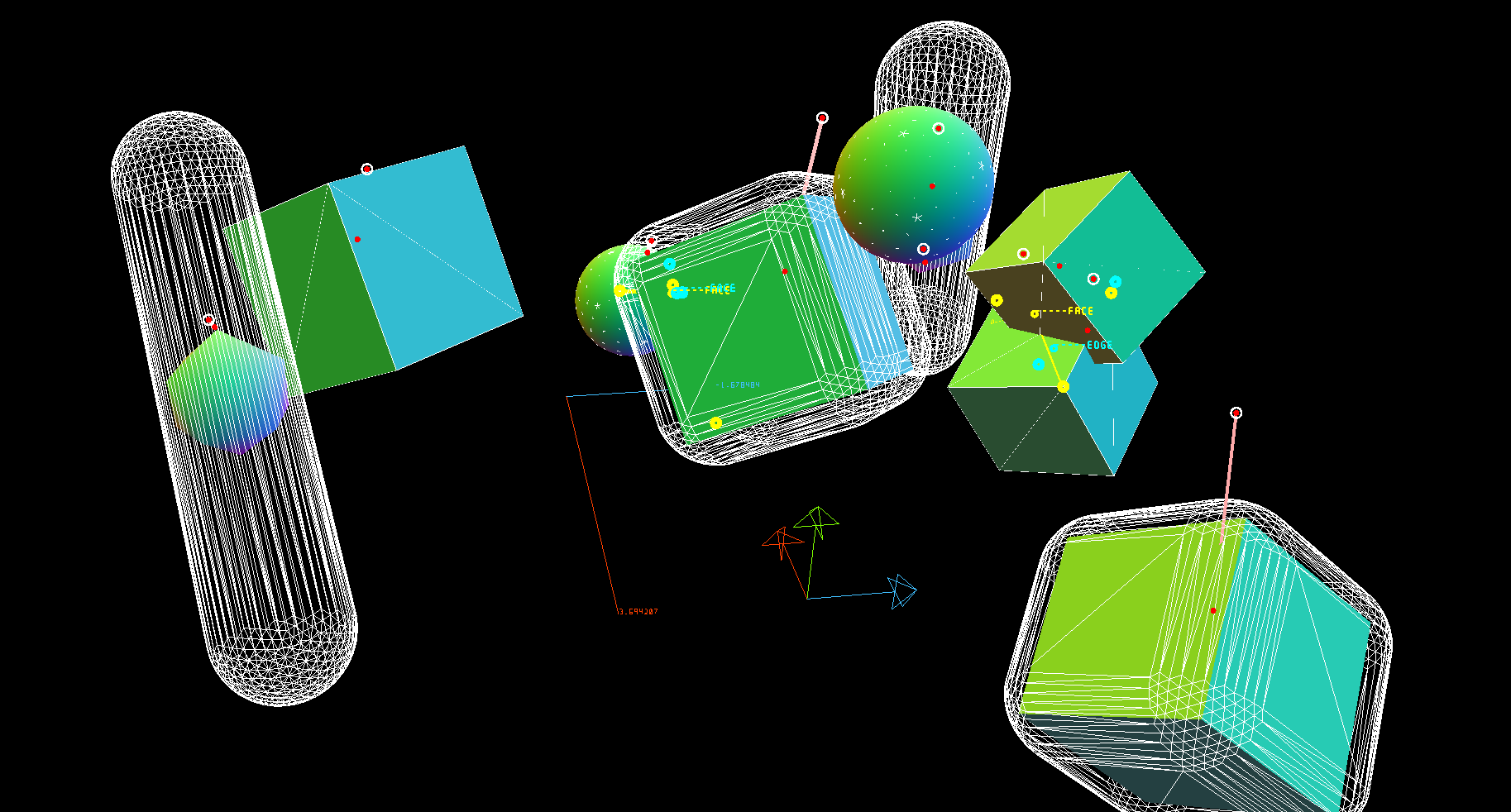
Here are a few more. Pay no heed to the intersecting cubes. Nor the tiny icosahedrons inside the capsule shapes.

Notes:

• The find_furthest(direction) functions are fairly simple, especially with the convention that direction is given in the space of the object. For a point primitive, for example, find_furthest will always return the origin. For a line segment, it will always return one of the endpoints (whichever is most aligned with direction). For a sphere, it will return a vector of the length of its radius, aligned with direction.

• Minkowski sums are easily obtained by simply adding the results of the find_furthest functions of two primitives.

• I have not yet implemented the idea in full - my current implementation is naive and results in some overlapping vertexes and duplicate triangles. I might post some code once I give it another pass.

• I’m not sure this is the best way to achieve debug meshes for geometry defined with a find_furthest function, but it’s my best idea for now. Please comment if you’ve got an idea or know a better way :)